مساحت مثلث: از مقدمات تا کاربردها
مثلث یکی از مهم ترین اشکال هندسی است که در دنیای اطراف ما به وفور دیده می شود. از طراحی ساختمان ها و پل ها تا الگوهای طبیعت مثلث نقش مهمی در مهندسی و معماری ایفا می کند. اما شاید تاکنون به این موضوع فکر نکرده باشید که چگونه می توان مساحت این شکل ساده اما پرکاربرد را محاسبه کرد؟ در این مقاله به طور کامل و مرحله به مرحله روش های محاسبه مساحت مثلث را بررسی می کنیم و به برخی از کاربردهای این فرمول می پردازیم.
فرمول پایه: قاعده ضربدر ارتفاع تقسیم بر دو
ابتدا به فرمول اصلی محاسبه مساحت مثلث می پردازیم. این فرمول از دوران دبستان برای شما آشناست:
مساحت مثلث = (قاعده × ارتفاع) / 2
اما این فرمول به چه معناست؟
قاعده: به هر یک از اضلاع مثلث می توانیم به عنوان قاعده نگاه کنیم.
ارتفاع: ارتفاع خطی عمود است که از رأس مقابل قاعده به قاعده رسم می شود.
مثال: فرض کنید یک مثلث با قاعده 10 سانتی متر و ارتفاع 5 سانتی متر داریم. با قرار دادن این اعداد در فرمول مساحت مثلث برابر با (10 × 5) / 2 = 25 سانتی متر مربع خواهد بود.
روش های مختلف محاسبه مساحت مثلث
برای محاسبه مساحت مثلث روش های مختلفی وجود دارد. هر یک از این روش ها به ویژگی های خاصی از مثلث وابسته است:
1. مثلث قائم الزاویه
برای مثلث قائم الزاویه محاسبه مساحت ساده تر است. به دلیل وجود زاویه قائمه یکی از اضلاع به عنوان ارتفاع و دیگری به عنوان قاعده به کار می رود:
مساحت مثلث قائم الزاویه = (ضلع قائم × ضلع قائم دیگر) / 2
مثال: یک مثلث قائم الزاویه با ضلع های 3 و 4 سانتی متر دارد. مساحت این مثلث (3 × 4) / 2 = 6 سانتی متر مربع است.
2. مثلث متساوی الاضلاع
در مثلث متساوی الاضلاع هر سه ضلع با هم برابر هستند. برای محاسبه مساحت از فرمول زیر استفاده می کنیم:
مساحت مثلث متساوی الاضلاع = (√3 / 4) × (ضلع)²
مثال: مثلث متساوی الاضلاع با ضلع 6 سانتی متر دارد. مساحت این مثلث برابر با (√3 / 4) × 6² = 9√3 سانتی متر مربع است.
3. مثلث با استفاده از طول اضلاع
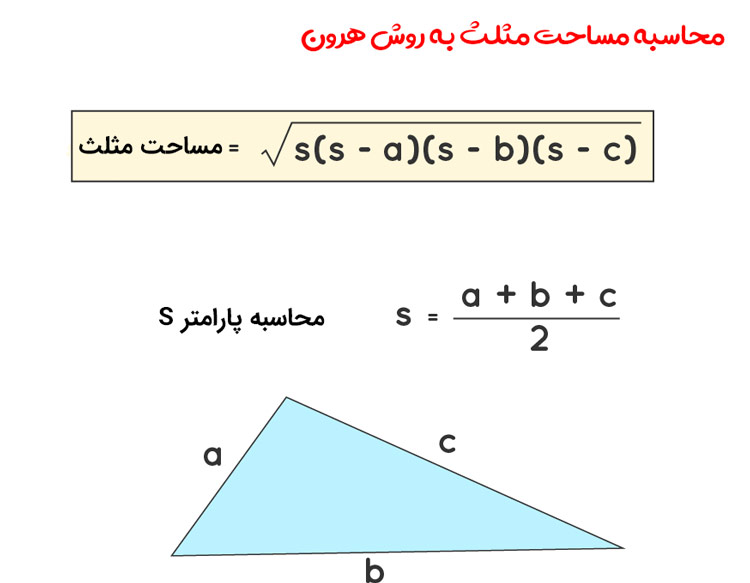
در مواردی که ارتفاع مثلث را نمی دانیم می توانیم از فرمول هِرون برای محاسبه مساحت استفاده کنیم. این فرمول از طول اضلاع مثلث برای محاسبه مساحت استفاده می کند.
فرمول هِرون:
- محیط مثلث را محاسبه کنید: محیط مثلث برابر با مجموع طول اضلاع است.
- نیم محیط را محاسبه کنید: نیم محیط برابر با نصف محیط مثلث است.
- فرمول هِرون را استفاده کنید: مساحت = √(s × (s-a) × (s-b) × (s-c))
- s: نیم محیط مثلث
- a, b, c: طول اضلاع مثلث
مثال: مثلثی با اضلاع 5 7 و 8 سانتی متر داریم.
- محیط = 5 + 7 + 8 = 20 سانتی متر
- نیم محیط = 20 / 2 = 10 سانتی متر
- مساحت = √(10 × (10-5) × (10-7) × (10-8)) = √(10 × 5 × 3 × 2) = √300 ≈ 17.32 سانتی متر مربع
4. مثلث با استفاده از مختصات
اگر مختصات سه رأس مثلث را بدانیم می توانیم از فرمول محدوده مثلث برای محاسبه مساحت استفاده کنیم.
فرمول محدودة مثلث:
مساحت = 1/2 * |(x1(y2-y3) + x2(y3-y1) + x3(y1-y2))|
- (x1, y1), (x2, y2), (x3, y3): مختصات سه رأس مثلث
مثال: مثلثی با رأس های A(1, 2), B(4, 3), C(2, 5) دارد.
- مساحت = 1/2 * |(1(3-5) + 4(5-2) + 2(2-3))|
- مساحت = 1/2 * |(-2 + 12 – 2)|
- مساحت = 1/2 * |8| = 4 واحد مربع
جدول مقایسه روش های محاسبه مساحت مثلث
| روش محاسبه | شرایط استفاده | فرمول | مثال | ||||
|---|---|---|---|---|---|---|---|
| قاعده × ارتفاع / 2 | همه انواع مثلث | مساحت = (قاعده × ارتفاع) / 2 | مثلثی با قاعده 8 و ارتفاع 5: مساحت = (8 × 5) / 2 = 20 | ||||
| مثلث قائم الزاویه | فقط برای مثلث قائم الزاویه | مساحت = (ضلع قائم × ضلع قائم دیگر) / 2 | مثلثی با اضلاع قائم 3 و 4: مساحت = (3 × 4) / 2 = 6 | ||||
| مثلث متساوی الاضلاع | فقط برای مثلث متساوی الاضلاع | مساحت = (√3 / 4) × (ضلع)² | مثلثی با ضلع 6: مساحت = (√3 / 4) × 6² = 9√3 | ||||
| فرمول هِرون | همه انواع مثلث | مساحت = √(s × (s-a) × (s-b) × (s-c)) | مثلثی با اضلاع 5 7 8: مساحت = √(10 × 5 × 3 × 2) ≈ 17.32 | ||||
| فرمول محدودة مثلث | همه انواع مثلث با مختصات رأس ها | مساحت = 1/2 * | (x1(y2-y3) + x2(y3-y1) + x3(y1-y2)) | مثلثی با رأس های A(1, 2), B(4, 3), C(2, 5): مساحت = 1/2 * | (1(3-5) + 4(5-2) + 2(2-3)) | = 4 |
کاربردهای محاسبه مساحت مثلث
محاسبه مساحت مثلث کاربردهای زیادی در زمینه های مختلف دارد:
- معماری و مهندسی: در طراحی ساختمان ها پل ها و سازه های دیگر محاسبه مساحت مثلث برای تعیین مقدار مواد مورد نیاز و محاسبه بارگذاری استفاده می شود.
- نقشه برداری: در نقشه برداری محاسبه مساحت زمین های مثلثی برای تعیین مساحت کل زمین استفاده می شود.
- فیزیک و ریاضیات: در فیزیک محاسبه مساحت مثلث برای محاسبه نیروی حاصل از فشار و در ریاضیات برای محاسبه حجم و مساحت سطوح سه بعدی استفاده می شود.
- علوم کامپیوتر: در علوم کامپیوتر محاسبه مساحت مثلث برای محاسبه حجم و مساحت اشکال سه بعدی در بازی های کامپیوتری و مدل سازی سه بعدی استفاده می شود.
نتیجه گیری
محاسبه مساحت مثلث یکی از مهارت های اساسی در ریاضیات و علوم کاربردی است. با استفاده از روش های مختلف می توانیم مساحت مثلث را به طور دقیق محاسبه کنیم. این فرمول ها در زمینه های مختلفی از جمله معماری مهندسی نقشه برداری فیزیک و علوم کامپیوتر کاربرد دارند.
پرسش و پاسخ
1. چگونه می توان ارتفاع مثلث را در هر نوع مثلثی پیدا کرد؟
در مثلث قائم الزاویه یکی از اضلاع به عنوان ارتفاع به حساب می آید. در دیگر انواع مثلث می توان از روش های هندسی مثل رسم عمود از رأس مقابل به قاعده برای پیدا کردن ارتفاع استفاده کرد.
2. چه تفاوتی بین فرمول هِرون و فرمول قاعده × ارتفاع / 2 وجود دارد؟
فرمول قاعده × ارتفاع / 2 برای محاسبه مساحت مثلث با داشتن قاعده و ارتفاع استفاده می شود. فرمول هِرون برای محاسبه مساحت مثلث با داشتن طول اضلاع استفاده می شود.
3. آیا می توانیم از فرمول محدودة مثلث برای محاسبه مساحت مثلثی با اضلاع نامنظم استفاده کنیم؟
بله. فرمول محدودة مثلث برای هر نوع مثلثی قابل استفاده است حتی مثلث های نامنظم.